Ví dụ về bài tập công thức Bernoulli

Câu trả lời chính xác nhất: Ví dụ bài tập công thức bernoulli là: Một lô hàng có tỷ lệ phế phẩm là 5%. Lấy ngẫu nhiên từ lô hàng đó ra 5 sản phẩm để kiểm tra (lấy có hoàn lại). Tìm xác suất để có 2 phế phẩm trong 5 sản phẩm lấy ra kiểm tra?

Giải: Ta coi việc kiểm tra một sản phẩm là thực hiện một phép thử. Vì kiểm tra 5 sản phẩm nên ta coi như thực hiện 5 phép thử độc lập. Gọi A là biến cố “sản phẩm lấy ra kiểm tra là phế phẩm”. Ta thấy trong mỗi phép thử chi có thể xảy ra một trong hai trường hợp: Hoặc sản phẩm kiểm tra là phế phẩm (tức A xảy ra), hoặc sản phẩm kiểm tra là sản phẩm tốt (tức A không xảy ra). Xác suất để A xảy ra trong mỗi phép thử đều bằng 0,05. Vậy các điều kiện để áp dụng công thức Bernoulli đều thoả mãn. Vì vậy, xác suất để có 2 phế phẩm trong 5 sản phẩm lấy ra kiểm tra là:

Để giúp các bạn hiểu hơn về câu hỏi Ví dụ về bài tập công thức bernoulli và một số kiến thức mở rộng khác liên quan tới công thức Bernoulli, Toploigiai đã mang tới bài mở rộng kiến thức sau đây, mời các bạn cùng tham khảo.

1. Giả thuyết Bernoulli là gì?

Daniel Bernoulli là nhà toán học của thế kỷ 19, đã đưa ra lời giải cho một nghịch lý nổi tiếng với cái tên “nghịch lý Xanh Pê-téc-bua”.

Vấn đề là phải lý giải tại sao con người không trả các khoản tiền cực lớn để chơi trò chơi sau đây: Một đồng tiền được tung lên, chẳng hạn cho đến khi mặt ngửa xuất hiện. nếu mặt ngửa xuất hiện ở lần tung thứ hai, người chơi nhận được 2² đơn vị tiền thưởng (ví dụ là 4 đồng). Nếu mặt ngửa xuất hiện ở lần tung thứ 3, người chơi nhận được 2³ đơn vị tiền thưởng, đến lần thứ tư người chơi nhận được 2⁴ đơn vị tiền thưởng, và vân vân. Tổng của xác suất nhận được tiền thưởng phải bằng 1, nhưng với số lần tung vô hạn, giá trị kỳ vọng của tiền thưởng cũng là một đại lượng vô hạn. Như vậy, người ta có thể nhận định rằng người chơi sẽ đánh những khoản tiền rất lớn trong một trò chơi như thế.

Giải thích tại sao mọi người chấp nhận chơi trò chơi này, Bernoulli lập luận rằng người chơi bạc quan tâm đến ích lợi của phần thưởng hơn là bản thân tiền thưởng. Bằng cách nêu ra giải thuyết về lợi ích cận biên giảm dần của thu nhập, Bernoulli chỉ ra rằng một trò chơi có thể có giá trị kỳ vọng bằng tiền vô hạn, nhưng có giá trị kỳ vọng tính bằng lợi ích hữu hạn. Bởi vậy mọi người quan tâm tới giả thuyết này trước hết vì nó là nỗ lực đầu tiên trong việc thay thế mục tiêu tính bằng tiền bằng sự tối ưu hóa lợi ích trong điều kiện có rủi ro hay tính bất định.

>>> Tham khảo: Công thức tổ hợp, chỉnh hợp, xác suất?

2. Phép thử Bernoulli và ứng dụng vào xác suất thống kê

Trước đó, vào thế kỳ 17, một nhà toán học nổi tiếng cũng thuộc nhà Bernoulli, Jacob Bernoulli đã phát minh ra phép thử Bernoulli. Dãy các phép thử Bernoulli được định nghĩa là đối với thí nghiệm ngẫu nhiên nào đó chúng ta thực hiện n lần

thử lặp lại. Chúng ta gọi dãy các phép thử này là dãy các phép thử Bernoulli nếu thoả mãn các điều kiện sau:

Đây là dãy các phép thử độc lập, nghĩa là kết quả của mỗi phép thử không

phụ thuộc vào kết quả của các phép thử khác.

Biến cố A xảy ra với xác suất p như nhau ở phép thử thứ i bất kỳ.

Nếu biến cố A xảy ra ở phép thử thứ i, ta nói phép thử thứ i thành công

Công thức của phép thử Bernoulli được viết như sau:

Công thức trên được dùng để tính Xác suất để biến cố A xuất hiện đúng k lần trong dãy n phép thử Bernoulli.

3. Ví dụ về bài tập công thức bernoulli

Ví dụ bài tập công thức bernoulli là: Một lô hàng có tỷ lệ phế phẩm là 5%. Lấy ngẫu nhiên từ lô hàng đó ra 5 sản phẩm để kiểm tra (lấy có hoàn lại). Tìm xác suất để có 2 phế phẩm trong 5 sản phẩm lấy ra kiểm tra?

Giải: Ta coi việc kiểm tra một sản phẩm là thực hiện một phép thử. Vì kiểm tra 5 sản phẩm nên ta coi như thực hiện 5 phép thử độc lập. Gọi A là biến cố “sản phẩm lấy ra kiểm tra là phế phẩm”. Ta thấy trong mỗi phép thử chi có thể xảy ra một trong hai trường hợp: Hoặc sản phẩm kiểm tra là phế phẩm (tức A xảy ra), hoặc sản phẩm kiểm tra là sản phẩm tốt (tức A không xảy ra). Xác suất để A xảy ra trong mỗi phép thử đều bằng 0,05. Vậy các điều kiện để áp dụng công thức Bernoulli đều thoả mãn. Vì vậy, xác suất để có 2 phế phẩm trong 5 sản phẩm lấy ra kiểm tra là:

---------------------------------

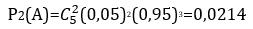
Trên đây Toploigiai đã mang tới cho các bạn câu trả lời chính xác nhất cho câu hỏi Ví dụ về bài tập công thức bernoulli và một số kiến thức mở rộng liên quan tới công thức bernoulli. Hi vọng những kiến thức mà chúng tôi cung cấp sẽ giúp các bạn học tập tốt hơn. Mời các bạn đến với câu hỏi tiếp theo.