Hoạt động 5 trang 108 Toán lớp 11 Cánh diều

Hoạt động 5 trang 108 Toán lớp 11 Cánh diều: Cho ba mặt phẳng song song (P), (Q), (R). Hai cát tuyến bất kì a và a’ cắt ba mặt phẳng song song lần lượt tại các điểm A, B, C và A’, B’, C’. Gọi B₁ là giao điểm của AC’ với mặt phẳng (Q) (Hình 66).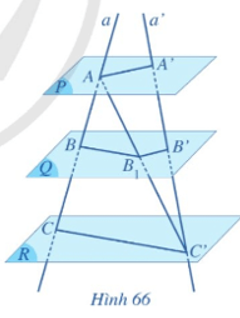

a) Nêu vị trí tương đối của BB₁ và CC’; B₁B’ và AA’.

b) Có nhận xét gì về các tỉ số

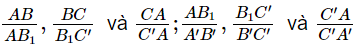
c) Từ kết quả câu a) và câu b), so sánh các tỉ số 

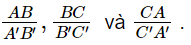
Lời giải:

a) Ta có: B ∈ (ACC’) và B ∈ (Q) nên B là giao điểm của (ACC’) và (Q); B₁ ∈ (ACC’) và B₁ ∈ (Q) nên B₁ là giao điểm của (ACC’) và (Q).

Do đó (ACC’) ∩ (Q) = BB₁.

Tương tự, ta có (ACC’) ∩ (R) = CC’.

Ta có: 

(Q) // (R);

(ACC’) ∩ (Q) = BB1;

(ACC’) ∩ (R) = CC’.

Suy ra BB1 // CC’.

Chứng minh tương tự ta cũng có: 

(P) // (Q);

(AA’C’) ∩ (P) = AA’;

(AA’C’) ∩ (Q) = B₁B’.

Suy ra B₁B’ // AA’.
b) Trong mp(ACC’), xét DACC’ có: BB₁ // CC’ nên theo định lí Thalès ta có: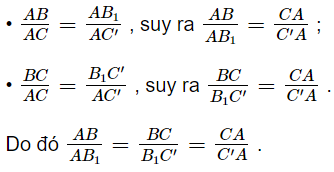

Trong mặt phẳng (AA’C’), xét AA’C’có: B₁B’ // AA’ nên theo định lí Thalès ta có: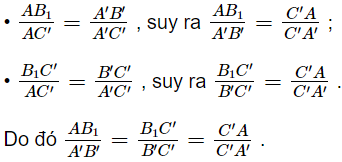

c) Theo chứng minh ở câu b ta có: