Bài 12 trang 72 SGK Toán 9 tập 2

Bài 2: Liên hệ giữa cung và dây

Bài 12 (trang 72 SGK Toán 9 tập 2)

Cho tam giác ABC . Trên tia đối của tia AB lấy một điểm D sao cho AD = AC. Vẽ đường tròn tâm O ngoại tiếp tam giác DBC. Từ O lần lượt hạ các đường vuông góc OH, OK với BC và BD (H ∈ BC, K ∈ BD)

a) Chứng minh rằng OH > OK.

b) So sánh hai cung nhỏ BD và BC.

Lời giải

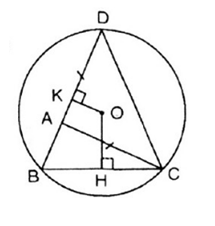
a) Xét ΔABC có: BC < AB + AC (Bất đẳng thức tam giác)

Mà AD = AC (gt)

⇒ BC < AB + AD = BD

Mà OH = khoảng cách từ O đến dây BC

OK = khoảng cách từ O đến dây BD

⇒ OH > OK.

b) Vì BD > BC

Tham khảo toàn bộ: Giải Toán 9