Bài 48 trang 77 SGK Toán 7 tập 2

Bài 7: Tính chất đường trung trực của một đoạn thẳng

Bài 48 (trang 77 SGK Toán 7 tập 2)

 Hai điểm M và N cùng nằm trên một nửa mặt phẳng bờ là đường thẳng xy. Lấy điểm L đối xứng với M qua xy. Gọi I là một điểm của xy. Hãy so sánh IM + IN với LN.

Lời giải:

Vì L và M đối xứng qua đường thẳng xy.

Nên đường thẳng xy là trung trực của ML.

I ∈ xy ⇒ IM = IL (theo định lý 1).

Nên IM + IN = IL + IN

- Trường hợp 1: Nếu I, L, N thẳng hàng

⇒ IL + IN = LN (vì N và L nằm khác phía so với đường thẳng xy và I nằm trên xy).

⇒ IM + IN = LN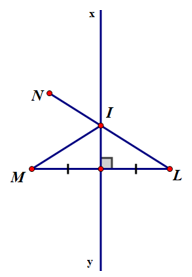

- Trường hợp 2: Nếu I không là giao điểm của LN và xy thì 3 điểm I, L, N không thẳng hàng

⇒ IL + IN > LN (bất đẳng thức tam giác)

⇒ IM + IN > LN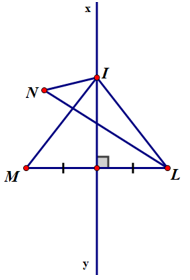

Vậy với mọi vị trí của I trên xy thì IM + IN ≥ LN

Xem toàn bộ Giải Toán 7: Luyện tập trang 76-77