Bài 41 trang 73 SGK Toán 7 tập 2

Bài 6: Tính chất ba đường phân giác của tam giác

Bài 41 (trang 73 SGK Toán 7 tập 2)

Hỏi trọng tâm của một tam giác đều có cách đều ba cạnh của nó hay không? Vì sao?

Lời giải: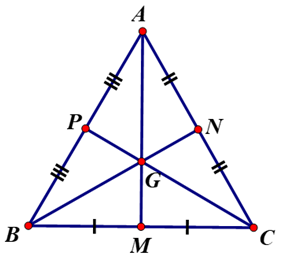

- Gọi G là trọng tâm ΔABC đều

AM, BN, CP là các đường trung tuyến của ΔABC

Theo tính chất trọng tâm tam giác ta có :

Vì ΔABC đều nên 3 trung tuyến AM = BN = CP (áp dụng chứng minh bài 29)

Suy ra: GA = GB = GC

Và AM – GA = BN – GB = CP – GC hay GM = GN = GP

- Xét ΔANG và ΔCNG có

GN chung

GA = GC (chứng minh trên)

NA = NC ( N là trung điểm AC)

Suy ra ΔANG = ΔCNG (c.c.c)

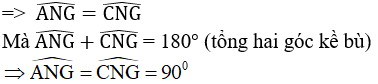
⇒ GN ⊥ AC tức là GN là khoảng cách từ G đến AC.

Chứng minh tương tự GM, GP là khoảng cách từ G đến BC, AB.

- Mà GM = GN = GP (chứng minh trên)

Vậy G cách đều 3 cạnh của tam giác ABC.

Xem toàn bộ Giải Toán 7: Luyện tập trang 73