Câu 11 trang 46 SGK Giải tích 12

Ôn tập chương I

Câu 11 trang 46 SGK Giải tích 12: 

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số 

b) Chứng minh rằng với mọi giá trị của đường thẳng y = 2x + m luôn cắt (C) tại hai điểm phân biệt M và N.

c) Xác định m sao cho độ dài MN nhỏ nhất.

d) Tiếp tuyến tại một điểm S bất kì của C cắt hai tiệm cận của C tại P và Q. Chứng minh rằng S là trung điểm của PQ.

Lời giải:

a) Khảo sát hàm số 

- TXĐ: D = R \ {-1}

- Sự biến thiên:

+ Chiều biến thiên:

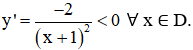
⇒ Hàm số nghịch biến trên các khoảng (-∞; -1) và (-1; +∞).

+ Cực trị: Hàm số không có cực trị.

+ Tiệm cận:

⇒ x = -1 là tiệm cận đứng của đồ thị hàm số.

⇒ y = 3 là tiệm cận đứng của đồ thị hàm số.

+ Bảng biến thiên:

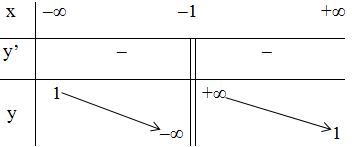
- Đồ thị:

+ Giao với Ox: (-3; 0)

+ Giao với Oy: (0; 3)

+ Đồ thị hàm số nhận (-1; 1) là tâm đối xứng.

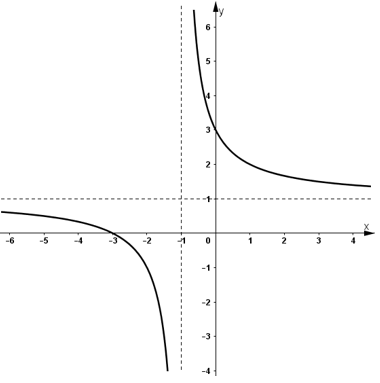
b) Phương trình hoành độ giao điểm của (C) và đường thẳng (d) y = 2x + m là:

⇔ (2x + m)(x + 1) = x + 3

⇔ 2x² + mx + 2x + m = x + 3

⇔ 2x² + (m + 1)x + m – 3 = 0 (*)

(d) cắt (C) tại hai điểm phân biệt

⇔ (*) có hai nghiệm phân biệt

⇔ Δ = (m + 1)² – 8(m – 3) > 0

⇔ m² – 6m + 25 > 0

⇔ (m – 3)² + 16 > 0

Đúng với ∀ m ∈ R.

Vậy với mọi m ∈ R, (d) cắt (C) tại hai điểm phân biệt MN.

c) Gọi M(x_M; y_M); N(x_N; y_N)

⇒ x_M; x_N là nghiệm của phương trình (*).

Theo hệ thức Vi-et ta có :

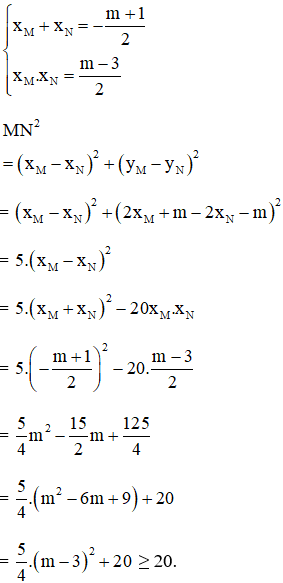
Dấu "=" xảy ra ⇔ m - 3 = 0 ⇔ m = 3

Vậy độ dài MN nhỏ nhất khi m = 3.

• Giải Toán 12: Ôn tập chương 1