Bài 17 trang 19 sgk Hình học 11 nâng cao

Bài 4: Phép quay và phép đối xứng tâm

Bài 17 (trang 19 sgk Hình học 11 nâng cao): 

Cho hai điểm B, C cố định trên đường tròn (O; R) và một điểm A thay đổi trên đường tròn đó. Hãy dùng phép đối xứng tâm để chứng minh rằng trực tâm H của tam giác ABC nằm trên một đường tròn cố định

Hướng dẫn. Gọi I là trung điểm của BC. Hãy vẽ đường kính AM của đường tròn rồi chứng minh rằng I là trung điểm của đoạn thẳng HM

Lời giải:

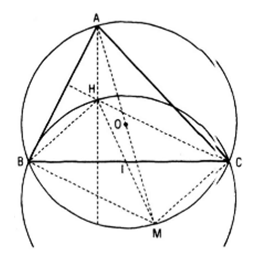
Ta vẽ đường kính AM của đường tròn.

Khi đó đường thẳng BH // đường thẳng MC (vì cùng vuông góc với đường thẳng AB) hay BHCM là hình bình hành, nếu gọi I là trung điểm của đường thẳng BC thì I cố định và cũng là trung điểm của đường thẳng BC thì I cố định và cũng là trung điểm của đường thẳng MH. Vậy phép đối xứng qua điểm I biến M thành H

Khi A chạy trên đường tròn (O; R) thì M chạy trên đường tròn (O; R). Do đó , H nằm trên đường tròn là ảnh của đường tròn (O; R) qua phép đối xứng tâm vơi tâm I.

Tham khảo toàn bộ: Giải Toán 11 nâng cao