Bài 6 trang 156 SGK Đại số 11
Bài 1: Định nghĩa và ý nghĩa của đạo hàm
Bài 6 trang 156 SGK Đại số 11
Viết phương trình tiếp tuyến của hypebol 
a) Tại điểm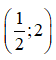 
;
b) Tại điểm có hoành độ bằng -1;
c) Biết rằng hệ số góc của tiếp tuyến bằng 
Lời giải
Hướng dẫn
a) Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm có hoành độ x = x0 là: y = f′(x0)(x − x0) + f(x0)
b) Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm có hoành độ x = x0 là: y = f′(x0)(x−x0) + f(x0)
c) Hệ số góc của tiếp tuyến tại điểm có hoành độ x0 là f′(x0)=3.
Giải phương trình tìm x0, từ đó viết phương trình tiếp tuyến của đồ thị hàm số y=f(x) tại điểm có hoành độ x=x0.
Ta có: Với mọi x0 ≠ 0:
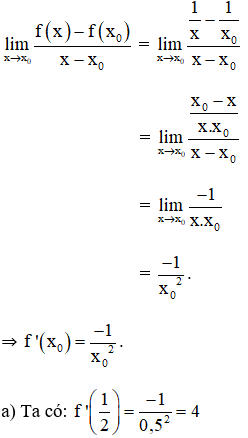
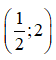⇒ Phương trình tiếp tuyến của đường cong tại điểm là:
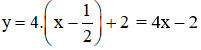
b) Tại x0= -1
⇒ y0 = -1
⇒ f’(x0) = -1.
Vậy phương trình tiếp tuyến của đường cong tại điểm có hoành độ -1 là:
y = -1(x + 1) – 1 = -x – 2.
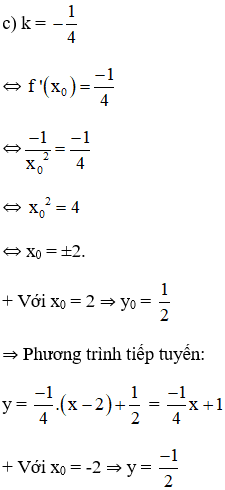
⇒ Phương trình tiếp tuyến:
Vậy có hai phương trình tiếp tuyến của hypebol có hệ số góc bằng:
Xem toàn bộ Giải Toán 11: Bài 1. Định nghĩa và ý nghĩa của đạo hàm
Xem thêm các bài cùng chuyên mục
Tham khảo các bài học khác
CÔNG TY TNHH TOP EDU
Số giấy chứng nhận đăng kí kinh doanh: 0109850622, cấp ngày 09/11/2021, nơi cấp Sở Kế Hoạch và Đầu tư Thành phố Hà Nội
