Bài 27 trang 85 SGK Đại Số 10 nâng cao

Luyện tập (trang 85)

Bài 27 (trang 85 SGK Đại Số 10 nâng cao)

Bằng cách đặt ẩn phụ, giải các phương trình sau:

a) 4x²– 12x – 5√(4x²– 12x + 11) + 15 = 0;

b) x²+ 4x – 3|x + 2| + 4 = 0;

c) 4x²+ 1/x²+ |2x – 1/x| - 6 = 0.

Lời giải:

a) Ta viết phương trình đã cho dưới dạng tương đương:

4x² – 12x + 11 – 5 √(4x² – 12x + 11) + 4 = 0

Đặt √(4x² – 12x + 11) = t (t ≥ 0) ta có phương trình:

t² – 5t + 4 = 0 ⇔ t = 1 hoặc t = 4.

Với t = 1 ⇒ √(4x² – 12x + 11) = 1 ⇔ 4x² – 12x – 10 = 0

⇔ 2x² – 6x + 5 = 0

Δ’ = 32 – 10 = - 1 < 0 nên phương trình này vô nghiệm.

Có Δ’ = 36 + 20 = 56, phương trình có hai nghiệm: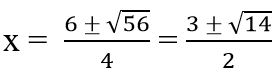

Các giá trị này đều là nghiệm của phương trình ban đầu

b) Ta viết phương trình về dạng tương đương :

|x + 2|2 -3|x + 2| = 0 (Vì |A|² = A² với mọi A)

Đặt |x + 2| = t( t ≥ 0), ta có phương trình :

t² – 3t = 0 ⇔ t = 0 hoặc t = 3

Với t = 0 ⇔ |x + 2| = 0 ⇔ x = -2

Với t = 3 ⇔ x + 2 = 3 hoặc x + 2 = -3 ⇔ x = 1 hoặc x = -5

Tóm lại, phương trình ban đầu có ba nghiệm : x = 1, x= - 5, x = -2

c) Ta viết phương trình về dạng tương đương:

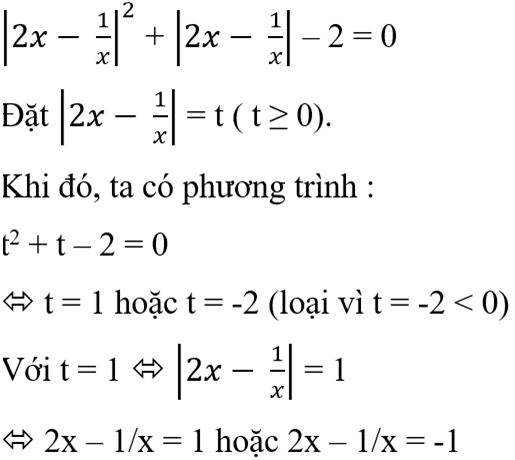
Giải các phương trình này ta có nghiệm của phương trình ban đầu là:

x = 1; x = -1/2 ; x = 1/2

Tham khảo toàn bộ: Giải bài tập Toán 10 nâng cao