Quy tắc phép chia đa thức cho đơn thức và các dạng bài tập hay gặp nhất

Hệ thống kiến thức về phép chia đa thức, cách giải bài tập chia đa thức cho đơn thức Toán 8 chi tiết, dễ hiểu bám sát chương trình Sách mới.

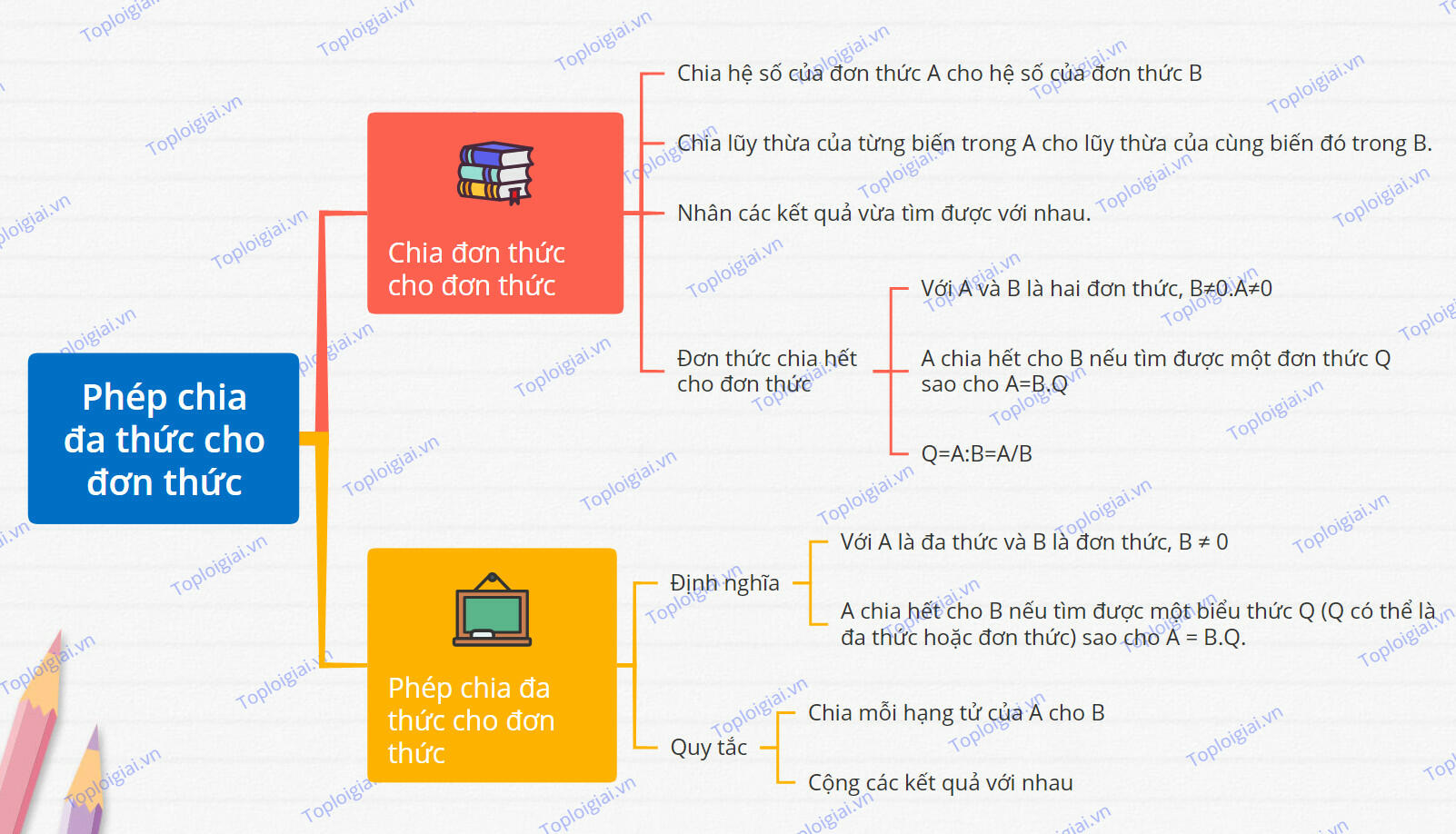
1. Quy tắc chia đơn thức cho đơn thức

* Để chia đơn thức A cho đơn thức B (trường hợp A chia hết cho B) ta có thể làm như sau:

- Chia hệ số của đơn thức A cho hệ số của đơn thức B. 

- Chia lũy thừa của từng biến trong A cho lũy thừa của cùng biến đó trong B. 

- Nhân các kết quả vừa tìm được với nhau.

* Đơn thức chia hết cho đơn thức khi:

Với A và B là hai đơn thức, B≠0.A≠0. Ta nói A chia hết cho B nếu tìm được một đơn thức Q sao cho A=B.Q

Kí hiệu: Q=A:B=A/B

2. Quy tắc phép chia đa thức cho đơn thức  

Định nghĩa: Với A là đa thức và B là đơn thức, B ≠ 0. Ta nói A chia hết cho B nếu tìm được một biểu thức Q (Q có thể là đa thức hoặc đơn thức) sao cho A = B.Q.

Trong đó:

A là đa thức bị chia.

B là đơn thức chia.

Q là thương .

Kí hiệu: Q = A : B hoặc A/B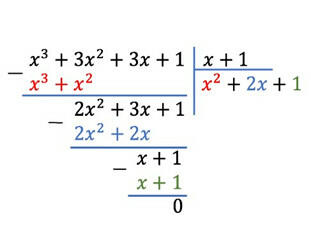

Quy tắc: Muốn chia đa thức A cho đơn thức B (trường hợp các hạng tử của đa thức A đều chia hết cho đơn thức B), ta chia mỗi hạng tử của A cho B rồi cộng các kết quả với nhau.

Chú ý: Trường hợp đa thức A có thể phân tích thành nhân tử, thường ta phân tích trước để rút gọn cho nhanh.

3. Hướng dẫn giải bài tập phép chia đa thức cho đơn 

* Ví dụ: Cho đa thức (x³ + 3x² + 3x + 1) : (x + 1)

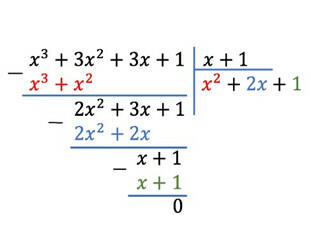
B1: Đầu tiên ta lấy x³ : x = x², ghi lại ở phần thương.

B2: Ta nhân x².(x + 1) = x³ + x²

Ta thực hiện phép trừ đa thức thu được 2x² + 3x +1.

B3: Ta tiếp tục chia 2x² : x = 2x rồi nhân 2x(x +1) = 2x² + 2x

Ta thực hiện phép trừ đa thức thu được x + 1. 

B4: Ta tiếp tục chia x : x = 1, ghi 1 rồi nhân 1.(x+1) = x+ 1. 

Ta thực hiện phép trừ đa thức thu được số dư bằng 0. 

Sơ đồ tư duy Phép chia đa thức cho đơn thức