Bài 2 trang 113 Toán lớp 11 Cánh diều

Bài 2 trang 113 Toán lớp 11 Cánh diều: Cho hình hộp ABCD.A'B'C'D'. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh BC, AA', C'D', AD'. Chứng minh rằng:

a) NQ // A'D' và NQ = 1/2 A'D';

b) Tứ giác MNQC là hình bình hành;

c) MN // (ACD');

d) (MNP) // (ACD').

Lời giải:

a)

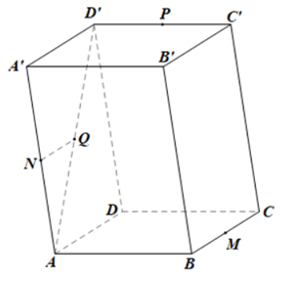
Ta có: N là trung điểm của AA' nên AN/AA′=1/2

Q là trung điểm của AD' nên AQ/AD′=1/2

Theo định lí Ta-lét ta có: NQ // A'D'

Suy ra: NQ/A′D′=AN/AA′=1/2 nên NQ=1/2A′D′

b)

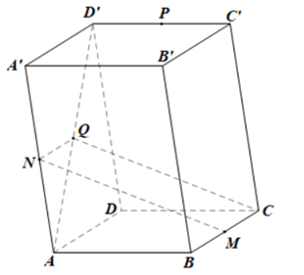
Ta có: NQ // A'D' mà A'D' // BC nên NQ // BC hay NQ // MC (1)

Ta có: NQ=1/2A′D′ mà A'D' = BC, MC = 1/2 BC nên NQ = MC (2)

(1)(2) suy ra: MNQC là hình bình hành

c)

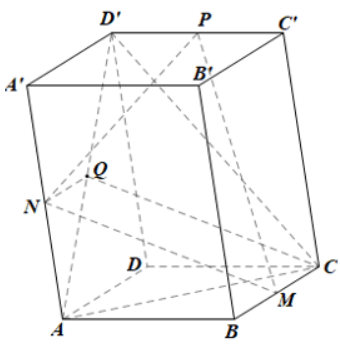
Ta có: MNCQ là hình bình hành nên MN // CQ

Mà CQ thuộc (ACD') 

Nên MN // (ACD')

d) 
 

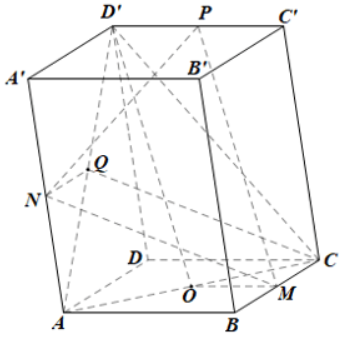
Gọi O là trung điểm của AC

△ACB có: O, M là trung điểm của AC, BC 

Suy ra: OM // AB nên OM = 1/2 AB 

Mà AB = C'D', D'P = 1/2 C'D 

Suy ra: OM = D'P (1)

Ta có: OM // AB, AB // C'D' nên OM // C'D' hay OM // D'P (2)

(1)(2) suy ra OMPD' là hình bình hành. Do đó: MP // OD'

Mà OD' thuộc (ACD') 

Suy ra: MP // (ACD') 

Mà MN thuộc (ACD') (câu c) 

Do đó: (MNP) // (ACD').