Bài 1 trang 113 Toán lớp 11 Cánh diều

Bài 1 trang 113 Toán lớp 11 Cánh diều: Cho hình hộp ABCD.A'B'C'D'. a) Chứng minh rằng (ACB') // (A'C'D).

b) Gọi G₁,G₂ lần lượt là giao điểm của BD' với các mặt phẳng (ACB') và (A'C'D). Chứng minh rằng G₁,G₂ lần lượt là trọng tâm của hai tam giác ACB' và A'C'D.

c) Chứng minh rằng BG₁=G₁G₂=D′G₂.

Lời giải:

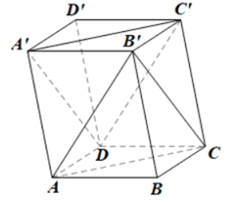
a) Ta có: AD // B'C', AD = B'C' nên ADC'B' là hình bình hành

Suy ra: AB' // DC' nên AB' // (A'C'D) (1)

Ta có: (ACC'A') là hình bình hành nên AC // A'C'. Suy ra: AC // (A'C'D) (2)

Mà AB', AC thuộc (ACB') (3)

(1)(2)(3) suy ra (ACB') // (A'C'D)

b)

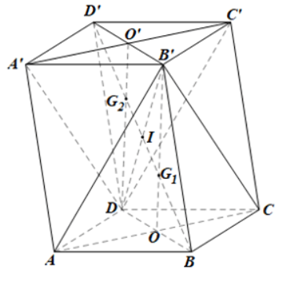
Gọi O, O' lần lượt là tâm hình bình hành ABCD, A'B'C'D'

Trong (BDD'B'): B'O cắt BD' mà B'O thuộc (ACB'), BD' cắt (ACB') tại G₁

Suy ra: B'O cắt BD' tại G₁

Tương tự ta có: DO' cắt BD' tại G₂

Ta có: △G₁OB đồng dạng với △G₁B'D' (do BD // B'D')

Suy ra: G₁O/G₁B′=OB/B′D′=1/2

Nên: G₁O/OB′=2/3

Do đó: G₁ là trọng tâm △ACB'.

Chứng minh tương tự ta có: G₂ là trọng tâm △A'C'D.

c) Ta có: △G₁OB đồng dạng với △G₁B'D'

Suy ra: G₁B/G₁D′=OB/B′D′=1/2

Nên: G₁B=1/3.BD′ (1)

Tương tự ta có: G₂D′/G₂B=OD′/DB=1/2

Nên: G₂D′=1/3.DD′ (2)

(1)(2) suy ra G₁B=G₁G₂=G₂D′.