3 mẫu Sơ đồ tư duy bài mệnh đề Toán 10
Tóm tắt lý thuyết Sơ đồ tư duy mệnh đề chi tiết nhất. Hướng dẫn cách vẽ Sơ đồ tư duy mệnh đề đẹp nhất.
1. Sơ đồ tư duy mệnh đề Toán 10
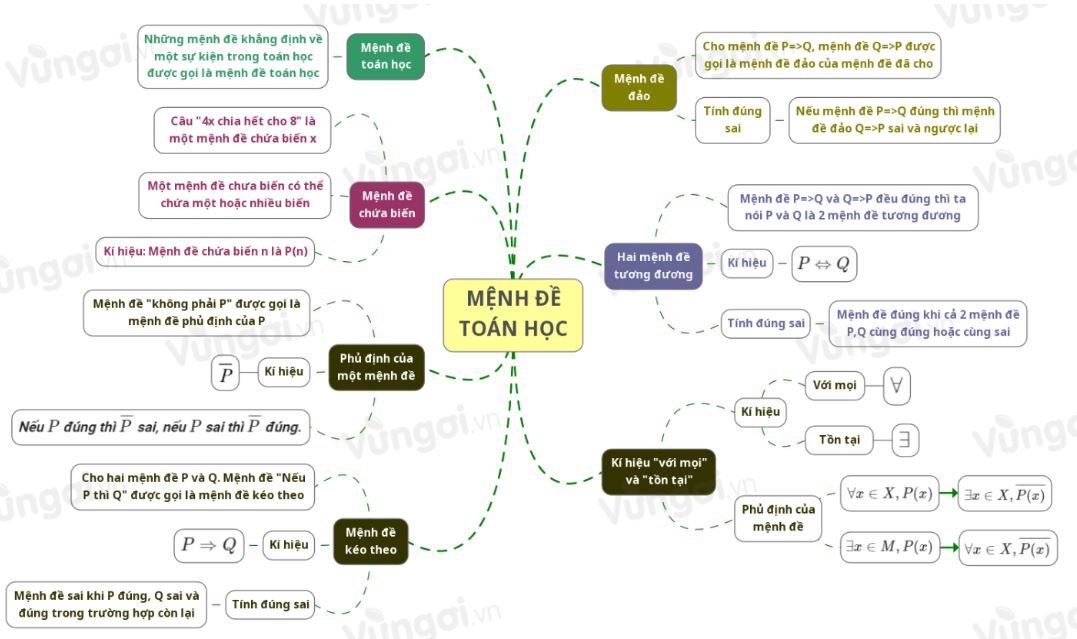
Mẫu 1
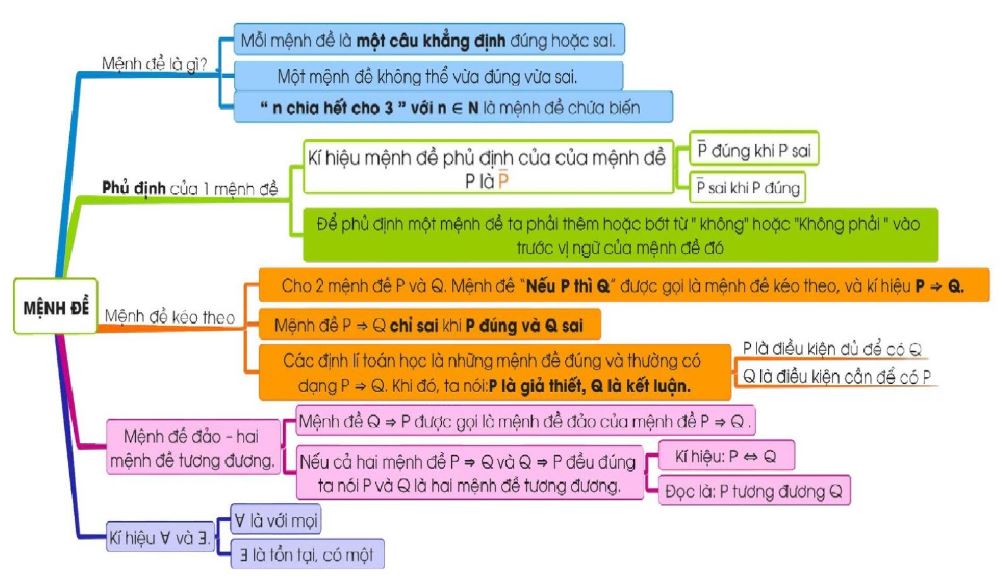
Mẫu 2
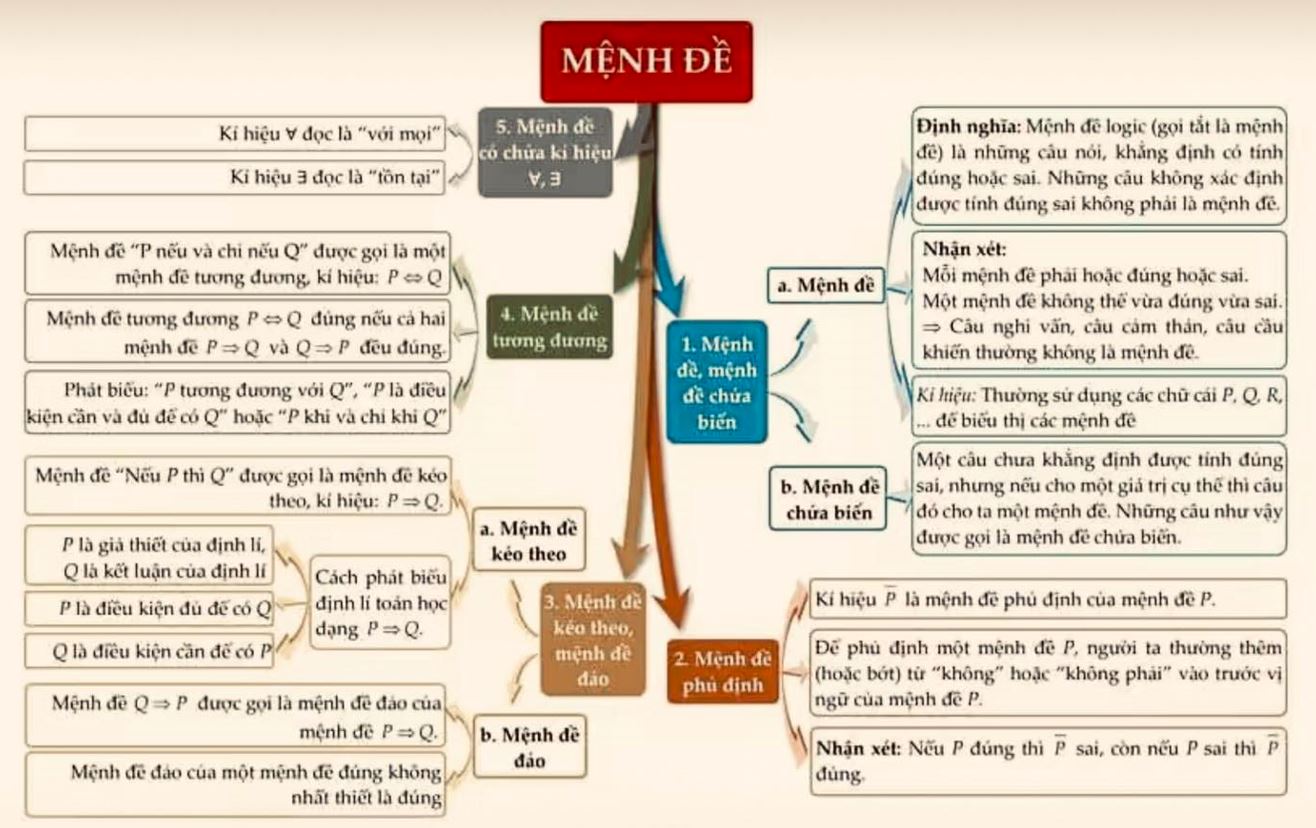
Mẫu 3
2. Định nghĩa Mệnh đề
Trong logic toán, một phân ngành logic, cơ sở của mọi ngành toán học, mệnh đề, hay gọi đầy đủ là mệnh đề logic là một khái niệm nguyên thủy, không định nghĩa.
Thuộc tính cơ bản của một mệnh đề là giá trị chân lý của nó, được quy định như sau:
Mỗi mệnh đề có đúng một trong hai giá trị chân lý 0 hoặc 1. Mệnh đề có giá trị chân lý 1 là mệnh đề đúng, mệnh đề có giá trị chân lý 0 là mệnh đề sai.
Ký hiệu:
- Người ta thường dùng các chữ cái a, b, c,... để ký hiệu cho các mệnh đề.
- Nếu mệnh đề a có giá trị chân lý là 1 thì ta ký hiệu G(a) = 1; nếu mệnh đề a có giá trị chân lý là 0 thì ta ký hiệu là G(a) = 0.
Chẳng hạn, để ký hiệu a là mệnh đề "Paris là thủ đô của nước Pháp" ta sẽ viết:
- a = "Paris là thủ đô của nước Pháp" hoặc
- a: "Paris là thủ đô của nước Pháp".
Ở đây, a là mệnh đề đúng nên G(a) = 1.
Chú ý:
1. Trong thực tế có những mệnh đề mà tính đúng sai của nó luôn gắn với một thời gian và địa điểm cụ thể: đúng ở thời gian hoặc địa điểm này nhưng sai ở thời gian hoặc địa điểm khác. Nhưng ở bất kì thời điểm nào, địa điểm nào cũng luôn có giá trị chân lý đúng hoặc sai. Chẳng hạn:
- Sáng nay bạn An đi học.
- Trời mưa.
- Học sinh tiểu học đang đi nghỉ hè.
2. Ta thừa nhận các luật sau đây của logic mệnh đề:
- Luật bài trùng: Mỗi mệnh đề phải hoặc đúng, hoặc sai; không có mệnh đề nào không đúng cũng không sai.
- Luật mâu thuẫn: Không có mệnh đề nào vừa đúng lại vừa sai.
3. Có những mệnh đề mà ta không biết (hoặc chưa biết) đúng hoặc sai nhưng biết "chắc chắn" nó nhận một giá trị. Chẳng hạn:
- Trên Sao Hỏa có sự sống.
3. Đặc điểm của mệnh đề
1. Mệnh đề là câu khẳng định có thể xác định được tính đúng hay sai của nó. Một mệnh đề không thể vừa đúng, vừa sai. Trong toán học, khi có hai số, người ta dùng các phép toán số học (cộng, trừ, nhân, chia,...) tác động vào chúng để nhận được những số mới. Tương tự, khi có mệnh đề, người ta dùng các phép logic tác động vào chúng để nhận được những mệnh đề mới. Dưới đây ta trình bày định nghĩa và các tính chất cơ bản của các phép toán này.
2. Mệnh đề chứa biến là câu khẳng định mà sự đúng hay sai của nó còn tùy thuộc vào một hay nhiều yếu tố biến đổi.
Ví dụ: Câu "Số nguyên n chia hết cho 3" không phải là mệnh đề, vì không thể xác định được nó đúng hay sai.
Nếu ta gán cho n giá trị n=4 thì ta có thể có một mệnh đề sai.
Nếu gán cho n giá trị n=9 thì ta có một mệnh đề đúng.
3. Phủ định của một mệnh đề A, là một mệnh đề, kí hiệu là A¯. Hai mệnh đề A và ¯¯¯A¯ là hai câu khẳng định trái ngược nhau.
Nếu A đúng thì A¯ sai.
Nếu A sai thì A¯ đúng.
Bảng giá trị chân lý của phép phủ định | |
a |
ā |
1 |
0 |
0 |
1 |
Ví dụ: Cho mệnh đề A: "5 là số nguyên tố".
Đây là mệnh đề đúng.
Mệnh đề phủ định: "5 không là số nguyên tố"
Đây là mệnh đề sai.
4. Mệnh đề kéo theo
Mệnh đề kéo theo có dạng: "Nếu A thì B", trong đó A và B là hai mệnh đề. Mệnh đề "Nếu A thì B" kí hiệu là A⇒B. Tính đúng, sai của mệnh đề kéo theo như sau:
Mệnh đề A⇒B chỉ sai khi A đúng và B sai.
Bảng giá trị chân lý của phép kéo theo | ||
a |
b |
a => b |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
Chú ý: Mệnh đề a kéo theo b thường được diễn đạt dưới nhiều hình thức khác nhau, chẳng hạn:
"Nếu a thì b"
"Có b khi có a"
"Từ a suy ra b"
"a là điều kiện đủ để có b"
"b là điều kiện cần (ắt có) để có a"
Ví dụ: Cho hai mệnh đề A:"3 chia hết cho 2" và B:"4 là số chẵn"
Khi đó A⇒B phát biểu là: "Nếu 3 chia hết cho 2 thì 4 là số chẵn"
Đây là mệnh đề đúng vì A sai, B đúng. (Mệnh đề A sai nhưng không ảnh hướng đến tính đúng của mệnh đề B nên mệnh đề kéo theo vẫn đúng).
5. Mệnh đề đảo
Mệnh đề "B⇒A " là mệnh đề đảo của mệnh đề A⇒B. Mệnh đề này chỉ sai khi B đúng, A sai.
Ví dụ: Trong ví dụ trên, mệnh đề B⇒A phát biểu là: "Nếu 4 là số chẵn thì 3 chia hết cho 2"
Mệnh đề này sai vì B đúng, A sai.
6. Mệnh đề tương đương
Nếu A⇒B là một mệnh đề đúng và mệnh đề B⇒A cũng là một mệnh đề đúng thì ta nói A tương đương với B, kí hiệu: A⇔B.
Khi A⇔B, ta cũng nói A là điều kiện cần và đủ để có B hoặc A khi và chỉ khi B hay A nếu và chỉ nếu BB.
Ví dụ: Cho hai mệnh đề A:"6 chia hết cho 2" và B:"4 là số chẵn"
Khi đó mệnh đề A và B đều đúng nên A⇔B phát biểu là "6 chia hết cho 2 khi và chỉ khi 4 là số chẵn"
7. Kí hiệu ∀, kí hiệu ∃
Cho mệnh đề chứa biến: P(x), trong đó x là biến nhận giá trị từ tập hợp X.
- Câu khẳng định: Với mọi x thuộc X thì P(x) là mệnh đề đúng và được kí hiệu là: ∀x∈X:P(x).
- Câu khẳng định: Có ít nhất một x∈X (hay tồn tại x∈X) để P(x) là mệnh đề đúng, kí hiệu là ∃x∈X:P(x).
