Lý thuyết Toán 8 Bài 7. Trường hợp đồng dạng thứ ba

Bài 7. Trường hợp đồng dạng thứ ba

A. Lý thuyết

Trường hợp đồng dạng thứ ba: Cạnh – Góc – Cạnh

1.  Định nghĩa

Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng.

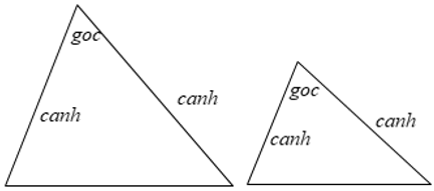
Tổng quát: ΔABC,ΔA'B'C' có A'B'/AB = A'C'/AC và Aˆ=A'ˆ

⇒ ΔABC ∼ Δ A'B'C' (c - g - c)

2.  Ví dụ áp dụng

Ví dụ: Cho tam giác ABC có AB=15cm, AC=20cm. Trên hai cạnh AB, AC lần lượt lấy 2 điểm E, D sao cho AD=8cm, AE=6cm. Chứng minh ΔAED ∼ ΔABC.

Hướng dẫn:

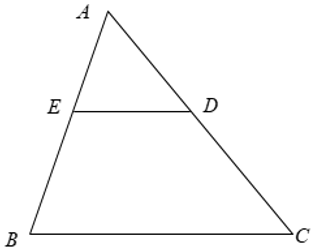
Xét ΔAED và ΔABC có:

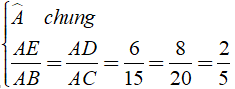
⇒ ΔAED ∼ ΔABC (c - g - c)

B. Một số dạng toán thường gặp

Dạng 1: Sử dụng tam giác đồng dạng để tính toán

Phương pháp: Ta sử dụng các tỉ lệ cạnh và các góc bằng nhau của hai tam giác đồng dạng để tính toán.

Dạng 2: Chứng minh hai tam giác đồng dạng và các hệ thức liên quan

Phương pháp: Ta sử dụng định lý: Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.

Dạng 3: Sử dụng tam giác đồng dạng để tính toán

Phương pháp:

+ Từ tam giác đồng dạng suy ra các cặp cạnh tỉ lệ và các góc bằng nhau

+ Từ đó tính cạnh và góc

Dạng 4: Chứng minh tam giác đồng dạng và các hệ thức liên quan

Phương pháp:

+ Sử dụng trường hợp đồng dạng thứ hai của tam giác để chứng minh tam giác đồng dạng

+ Từ đó suy ra các hệ thức cần chứng minh

Dạng 5: Sử dụng tam giác đồng dạng để tính toán

Phương pháp:

+ Từ tam giác đồng dạng suy ra các cặp cạnh tỉ lệ và các góc bằng nhau

+ Từ đó tính cạnh và góc

Dạng 6: Chứng minh tam giác đồng dạng và các hệ thức liên quan

Phương pháp:

+ Sử dụng trường hợp đồng dạng thứ ba của tam giác để chứng minh tam giác đồng dạng

+ Từ đó suy ra các hệ thức cần chứng minh.

Xem thêm Giải Toán 8: Bài 7. Trường hợp đồng dạng thứ ba