Lý thuyết Toán 8 Bài 7. Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức

Bài 7. Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức

A. Lý thuyết

1. Phương pháp dùng hằng đẳng thức

+ Dùng các hằng đẳng thức đáng nhớ để phân tích đa thức thành nhân tử.

+ Cần chú ý đến việc vận dụng linh hoạt các hằng đẳng thức để phù hợp với các nhân tử.

2. Ví dụ áp dụng

Ví dụ: Phân tích đa thức sau thành nhân tử

a, 9x² - 1

b, x² + 6x + 9.

Hướng dẫn:

a) Ta có: 9x² - 1 = (3x)² - 1² = (3x - 1)(3x + 1)

(áp dụng hằng đẳng thức A² - B² = (A - B)(A + B)

b) Ta có: x² + 6x + 9 = x² + 2.x.3 + 3² = (x + 3)².

(áp dụng hằng đẳng thức (A + B)² = A² + 2AB + B²

B. Một số dạng toán thường gặp

Dạng 1: Phân tích đa thức thành nhân tử

Phương pháp: Ta sử dụng các hằng đẳng thức đã học để phân tích đa thức đã cho thành nhân tử.

Dạng 2: Tìm x

Phương pháp: Ta sử dụng các hằng đẳng thức đã học để phân tích đa thức đã cho thành nhân tử.

Từ đó đưa về dạng tìm x thường gặp như

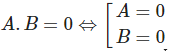
Dạng 3: Tính giá trị biểu thức thỏa mãn điều kiện cho trước

Phương pháp: Ta biến đổi biểu thức đã cho để có thể sử dụng được điều kiện ở giả thiết.
Từ đó tính giá trị biểu thức.

Xem thêm Giải Toán 8: Bài 7. Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức