Câu hỏi 4 trang 58 Toán 7 Tập 2 Bài 2

Bài 2: Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu

Câu hỏi 4 trang 58 Toán 7 Tập 2 Bài 2:

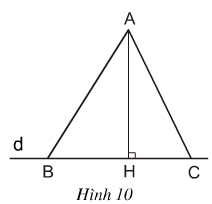
Cho hình 10. Hãy sử dụng định lí Py-ta-go để suy ra rằng:

a) Nếu HB > HC thì AB > AC;

b) Nếu AB > AC thì HB > HC;

c) Nếu HB = HC thì AB = AC, và ngược lại, nếu AB = AC thì HB = HC.

Lời giải

Xét tam giác AHB vuông tại H

Áp dụng định lí Py-ta-go ta có:

AB² = AH² + HB² (1)

Xét tam giác AHC vuông tại H

Áp dụng định lí Py-ta-go ta có:

AC² = AH² + HC² (2)

a) Nếu HB > HC ⇒ HB²> HC².

⇒ AH² + HB² > AH² + HC²

Kết hợp với  điều kiện (1) và (2)

⇒ AB² > AC²

⇒ AB > AC

b) AB > AC ⇒ AB²> AC²

Kết hợp với  điều kiện (1) và (2)

⇒ AH² + HB² > AH² + HC²

⇒ HB² > HC²

⇒ HB > HC

c) - Nếu HB = HC ⇒ HB²= HC².

⇒ AH² + HB² = AH² + HC²

Kết hợp với  điều kiện (1) và (2)

⇒ AB² = AC²

⇒ AB = AC

- Nếu AB = AC ⇒ AB² = AC²

Kết hợp với  điều kiện (1) và (2)

⇒ AH² + HB² = AH² + HC²

⇒ HB² = HC²

⇒ HB = HC

Xem toàn bộ Giải Toán 7: Bài 2. Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu