Bài 13 trang 60 SGK Toán 7 tập 2

Bài 2: Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu

Bài 13 (trang 60 SGK Toán 7 tập 2)

 Cho hình 16. Hãy chứng minh rằng:

a) BE < BC;

b) DE < BC.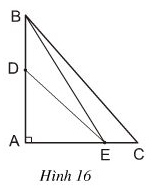

Lời giải:

a) Ta có: BE, BC là 2 đường xiên vẽ từ B đến đường AC.

BA ⏊ AC tại A nên A là hình chiếu của B trên AC

⇒ AE, AC lần lượt là hình chiếu của BE, BC.

Trong hình vẽ E nằm giữa A và C ⇒ AE < AC ⇒ BE < BC (đường xiên nào có hình chiếu lớn hơn thì lớn hơn).

b) Trong hình vẽ D nằm giữa A và B ⇒ AD < AB

Ta có: ED, EB là 2 đường xiên vẽ từ E đến đường AB

EA ⏊ AB tại A nên A là hình chiếu của E trên AB.

⇒ AD, AB lần lượt là hình chiếu của ED, EB trên AB

Trong hình vẽ D nằm giữa A và B ⇒ AD < AB nên ED < EB hay DE < BE (đường xiên nào có hình chiếu lớn hơn thì lớn hơn).

Kết hợp với kết quả ý a suy ra DE < BE < BC ⇒ DE < BC.

Xem toàn bộ Giải Toán 7: Luyện tập trang 59-60