Bài 32 trang 68 sgk Hình học 11 nâng cao

Bài 4: Hai mặt phẳng song song

Bài 32 (trang 68 sgk Hình học 11 nâng cao): 

Cho hai đường thẳng chéo nhau a và b lần lượt nằm trên hai mặt phẳng song song (P) và (Q). Chứng minh rằng nếu điểm M không nằm trên (P) và không nằm trên (Q) thì duy nhất một đường thẳng đi qua M cắt cả a và b

Lời giải:

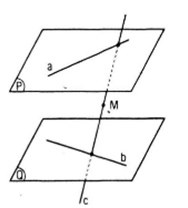
Giả sử đường thẳng c = mp(M, a) ∩ mp(M, b). Ta cần chứng minh đường thẳng c cắt cả đường thẳng a và đường thẳng b. Vì đường thẳng c và đường thẳng a cùng nằm trên một mặt phẳng và không thể trùng nhau (do đường thẳng c qua M và đường thẳng a không đi qua M) nên hoặc c // a hoặc c cắt b. Cũng vậy hoặc c // b hoặc c cắt b. Không thể xảy ra đồng thời c // a, c // b vì a, b chéo nhau. Vậy nếu đường thẳng c song song với đường thẳng a thì đường thẳng c phải cắt đường thẳng b , tức là đường thẳng c qua một điểm của mp(Q), và do đó M thuộc (Q) (trái giả thiết). Tương tự, không thể có c song song với b. Tóm lại c phải cắt a và b

Nếu còn có đường thẳng c’ khác đi qua M, cắt cả a và b thì a và b đồng phẳng. Vô lí

Tham khảo toàn bộ: Giải Toán 11 nâng cao