Bài 6.3 trang 165 sbt Toán 8 tập 1

Bài 6: Diện tích đa giác

Bài 6.3 trang 165 sbt Toán 8 tập 1

Bạn Giang đã vẽ một đa giác ABCDEFGHI như ở hình bs. 26.

Tính diện tích của đa giác đó, biết rằng : KH song song với BC (K thuộc EF); BC song song với GF; CF song song với BG; BG vuông góc với GF; CK song song với DE; CD song song với FE; KE = DE và KE vuông góc với DE; I là trung điểm của BH, AI = IH và AI vuông góc với IH; HK = 11cm, CF = 6cm. HK cắt CF tại J và JK = 3 (cm), JF = 2cm. BG cắt HK tại M và HM = 2cm.

Lời giải:

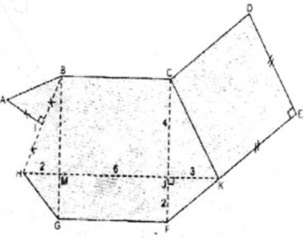
Chia đa giác đó thành hình vuông CDEK, hình thang KFGH, hình thang BCKH và tam giác vuông AIB

Ta có: MJ = KH – KJ – MH = 11 – 2 – 3 = 6(cm)

⇒ BC = GF = MJ = 6 (cm)

CJ = CF – FG = 6 – 2 = 4 (cm)

S_KFGH = (HK + GF)/2. FJ = (11 + 6)/2.2 = 17 (cm²)

S_BCKH = (BC + KH)/2. FJ = (11 + 6)/2.4 = 34 (cm²)

Trong tam giác vuông BMH có ∠J = 90^o .Theo định lý Pi-ta-go ta có:

CK²= CJ² + JK² = 16 + 9 = 25 ⇒ CK = 5 (cm)

S_CDEK = CK² = 5² = 25 (cm²)

Trong tam giác vuông BMH có ∠M = 90^o .Theo định lý Pi-ta-go ta có:

BH²= BM² + HM²

mà BM = CJ = 4(cm) (đường cao hình thang BCKH)

⇒ BH² = 4² + 2² = 20

IB = BH/2 ⇒ IB²= BH²/2 = 20/4 = 5

IB = √5 (cm)

ΔAIB vuông cân tại I (vì AI = IH = IB)

S_AIB = 1/2 AI. IB = 1/2 IB² = 5/2 (cm²)

S = S_CDEK + S_KFGH + S_BCKH + S_AIB = 25 + 17 + 34 + 5/2 = 157/2 (cm²)

 Xem toàn bộ Giải SBT Toán 8: Bài 6. Diện tích đa giác