Bài 6.2 trang 88 sbt Toán 8 tập 1
Bài 6: Đối xứng trục
Bài 6.2 trang 88 sbt Toán 8 tập 1
Cho tam giác ABC cân tại A. Trên tia đối của tia AB lấy điểm D, trên tia đối của tia AC lấy điểm E sao cho AD = AE. Gọi M là trung điểm của BC. Chứng minh rằng D đối xứng với E qua AM.
Lời giải:
Hướng dẫn
+) Trong tam giác cân, đường trung tuyến ứng với cạnh đáy cũng là đường trung trực, đường phân giác.
+) Sử dụng định nghĩa: Hai điểm gọi là đối xứng với nhau qua đường thẳng d nếu d là đường trung trực của đoạn thẳng nối hai điểm đó.
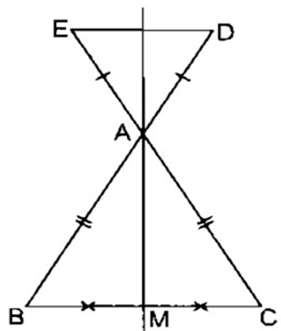
ΔABC cân tại A
AM là đường trung tuyến
⇒ AM là tia phân giác (BAC)
⇒ ∠(BAM) = ∠(MAC) (1)
Kéo dài MA cắt DE tai N, ta có:
∠(BAM) = ∠(DAN) (đối đỉnh) (2)
∠(MAC) = ∠(NAE) (đối đỉnh)(3)
Từ (1), (2) và (3) suy ra: ∠(DAN) = ∠(NAE)
ΔADE cân tại A có AN là tia phân giác
⇒ AN là đường trung trực của DE
hay AM là đường trung trực của DE
Vậy D đối xứng với E qua AM.
Xem toàn bộ Giải SBT Toán 8: Bài 6. Đối xứng trục
Câu hỏi thường gặp
Xem thêm các bài cùng chuyên mục
CÔNG TY TNHH TOP EDU
Số giấy chứng nhận đăng kí kinh doanh: 0109850622, cấp ngày 09/11/2021, nơi cấp Sở Kế Hoạch và Đầu tư Thành phố Hà Nội
