Bài 154 trang 99 sbt Toán 8 tập 1

Bài 12: Hình vuông

Bài 154 trang 99 sbt Toán 8 tập 1

Cho hình vuông ABCD, điểm E thuộc cạnh CD. Tia phân giác của góc ABB cắt CD ở K. Chứng minh rằng AK+CE = BE.

Lời giải:

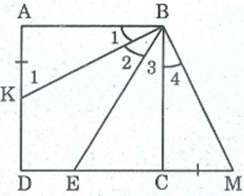
Trên tia đối của tia CD lấy điểm M sao cho CM = AK

Ta có: AK + CE = CM + CE = EM (1)

Xét ΔABK và ΔCBM, ta có:

AB = CB (gt)

∠A = ∠C = 90^o

AK = CM (theo cách vẽ)

Suy ra: ΔABK = ΔCBM (c.g.c)

⇒ ∠B₁ = ∠B₄ (2)

Mà ∠(KBC) = 90^o - ∠B₁ (3)

Tam giác CBM vuông tại C nên: ∠M = 90^o - ∠B₄ (4)

Từ (2), (3) và (4) suy ra: ∠(KBC) = ∠M (5)

Lại có: ∠(KBC) = ∠B₂ + ∠B₃ (gt)

Và ∠B₁ = ∠B₄ (chứng minh trên)

Suy ra: ∠B₂ = ∠B₄ (6)

Từ (5) và (6) suy ra: ∠(EBM) = ∠M

⇒ ΔEBM cân tại E ⇒ EM = BE. (7)

Từ (1) và (7) suy ra: AK + CE = BE.

Xem toàn bộ Giải SBT Toán 8: Bài 12. Hình vuông