Đề kiểm tra 1 tiết Toán 9 Chương 4 Đại số ( Đề 5)

Đề kiểm tra 1 tiết Toán 9 Chương 4 Đại số ( Đề 5)

Đề 5:

I. Phần trắc nghiệm (3 điểm)

Câu 1: Cho hàm số y = -1/2x² . Kết luận nào sau đây đúng?

A. Hàm số trên luôn đồng biến.

B. Hàm số trên luôn nghịch biến.

C. Giá trị của hàm số bao giờ cũng âm.

D. Hàm số trên đồng biến khi x < 0 và nghịch biến khi x > 0.

Câu 2: Điểm P(-1;-2) thuộc đồ thị hàm số y = -mx² khi m bằng:

A. 2       B.-2       C.4       D.-4

Câu 3: Biệt thức Δ’ của phương trình 4x² -6x - 1 = 0 là:

B. 52       B.13       C.5       D.10

Câu 4: Tập nghiệm của phương trình x² -5x - 6 = 0 là:

A. S = {1 ; -6}       B. S = {1 ;6}       C. S = {-1 ; 6}       D. S = {2 ;3}

Câu 5: Cho phương trình 3x² - 4x + m = 0. Giá trị m để phương trình có các nghiệm x₁, x₂ thỏa mãn x₁ - x₂ = 1 là:

A. m = -7/12       B. m = 7/12       C. m = 1       D. m = 1/3

Câu 6: Chọn câu có khẳng định sai.

A. Phương trình 200x²- 500x + 300 = 0 có hai nghiệm phân biệt là: x₁= 1 ; x₂ = 3/2

B. Phương trình 3x²- 12x – 15 = 0 có tổng các nghiệm số x₁+ x₂ = 4 và tích các nghiệm số x₁x₂ = -5

C. Phương trình x²+ 4x + 5 = 0 có tập nghiệm S = ∅

D. Hàm số y = 3x² đồng biến khi x < 0.

II. Phần tự luận (7 điểm)

Bài 1: (3 điểm) Cho hàm số y = ax² (a ≠ 0)

a) Xác định hệ số a biết đồ thị hàm số đi qua điểm A(-2; 2).

b) Vẽ đồ thị của hàm số ứng với giá trị a vừa tìm được ở câu trên.

Bài 2: (3 điểm)

1) Giải phương trình 2011x² - 2012x + 1 = 0

2) Cho phương trình bậc hai (ẩn x): x² - 2mx + 2m – 1 = 0

a) Với giá trị nào của m thì phương trình có nghiệm.

b) Xác định m để phương trình có nghiệm kép và tính nghiệm đó.

Bài 3: (1 điểm) Giả sử a;b là hai nghiệm của phương trình x² + mx + 1=0 và b;c là hai nghiệm của phương trình x² + nx + 2=0. Chứng minh hệ thức: (b-a)(b-c)=m.n-6.

Đáp án và thang điểm

I. Phần trắc nghiệm (3 điểm)

II. Phần tự luận (7 điểm)

Bài 1:

a) Vì đồ thị hàm số y = ax²đi qua điểm A(-2; 2) nên ta có:

2 = a.2² ⇒ 4a = 2 ⇒ a = 1/2

⇒ Hàm số cần tìm là y = 1/2 x²

b) Bảng giá trị:

Đồ thị hàm số y = 1/2x² là một đường Parabol nằm phía trên trục hoành, nhận trục tung làm trục đối xứng, nhận gốc tọa độ O(0;0) làm đỉnh và là điểm thấp nhất.

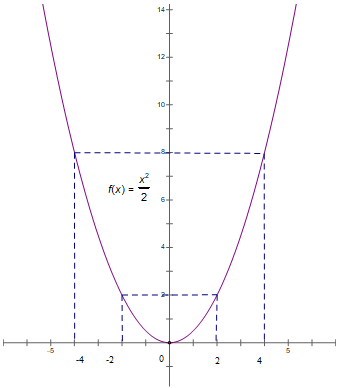
Bài 2:

1) Giải phương trình 2011x² - 2012x + 1 = 0

Ta có: a = 2011; b = -2012; c = 1

⇒ a + b + c = 0 ⇒ Phương trình có 2 nghiệm

x₁ = 1; x₂ = c/a = 1/2011

Vậy tập nghiệm của phương trình là : S = {1; 1/2011}

2) x² - 2mx + 2m – 1 = 0

Δ = b² - 4ac = (2m)² - 4.(2m - 1) = 4m² -8m + 4 = 4(m - 1)²

Do Δ = 4(m -1)² ≥ 0 ∀ m nên phương trình luôn có nghiệm với mọi m

Phương trình có nghiệm kép khi và chỉ khi

Δ = 0 ⇔ 4(m - 1)² = 0 ⇔ m = 1

Khi đó nghiệm kép của phương trình là:

x = (-b)/2a = 2m/2 = m = 1

Bài 3:

Vì a, b là 2 nghiệm của phương trình x² + mx + 1 = 0 nên theo định lí Vi-et ta có:

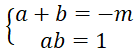
Vì b,c là 2 nghiệm của phương trình x² + nx + 2 = 0 nên theo định lí Vi-et ta có:

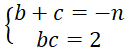
Khi đó:

(b – a)(b – c) = b² – bc – ab + ac

= b² + bc + ab + ac – 2(ab + bc)

= b( b + c) + a (b + c) – 2 (ab + bc)

= (b + c )( b + a) – 2 (ab + bc)

= (-n).(-m) – 2(1 + 2)

= nm – 6

Xem toàn bộ: Đề kiểm tra 1 tiết Toán 9 Chương 4 Đại số