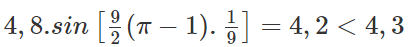Bài 14 trang 42 Toán lớp 11 Cánh diều

Bài 14 trang 42 Toán lớp 11 Cánh diều: Một cây cầu có dạng cung OA của đồ thị hàm số y=4,8.sinx/9 và được mô tả trong hệ trục tọa độ với đơn vị trục là mét như ở Hình 39.

a) Giả sử chiều rộng của con sông là độ dài đoạn thẳng OA. Tìm chiều rộng đó (làm tròn kết quả đến hàng phần mười).

b) Một sà lan chở khối hàng hóa được xếp thành hình hộp chữ nhật với độ cao 3,6 m so với mực nước sông sao cho sà lan có thể đi qua được gầm cầu. Chứng minh rằng chiều rộng của khối hàng hóa đó phải nhỏ hơn 13,1 m.

c) Một sà lan khác cũng chở khối hàng hóa được xếp thành hình hộp chữ nhật với chiều rộng của khối hàng hóa đó là 9 m sao cho sà lan có thể đi qua được gầm cầu. Chứng minh rằng chiều cao của khối hàng hóa đó phải nhỏ hơn 4,3 m.

Một sà lan chở khối hàng hóa được xếp thành hình hộp chữ nhật với độ cao 3,6 m so với mực nước sông sao cho sà lan có thể đi qua được gầm cầu. Chứng minh rằng chiều rộng của khối hàng hóa đó phải nhỏ hơn 13,1 m.

Lời giải:

a) Vì A nằm trên trục Ox nên tung độ của A = 0. Suy ra:

Vậy chiều rộng của con sông là 9π≈28,27(m)

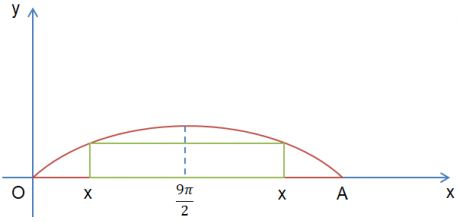
b)Sà lan có thể đi qua được gầm cầu khi và chỉ khi: 

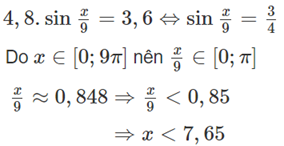
Ta có chiều rộng khối hàng hóa là: 2∣9π/2−x∣

Vì x<7,65 nên 2∣9π/2−x∣<12,97<13,1 (đcpcm)

c)  

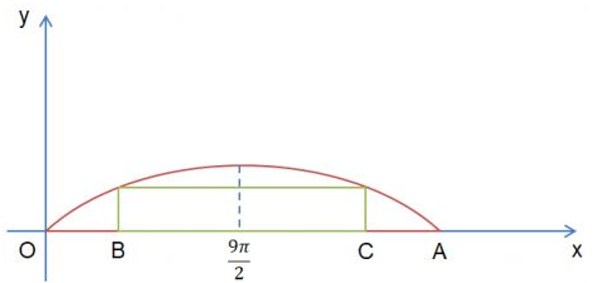
Ta có: BC = 9

Nên 2∣9π/2−x∣=9⇒x=9/2(π−1)

Do đó, chiều cao của khối hàng hóa là