Hoạt động 2 trang 67 Toán lớp 11 Cánh diều
Hoạt động 2 trang 67 Toán lớp 11 Cánh diều: Cho hàm số f(x) = x2 – 1, g(x) = x + 1.
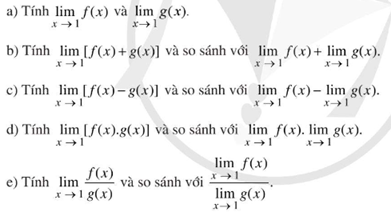
Lời giải:
a) Giả sử (xn) là dãy số bất kì thỏa mãn limxn = 1. Khi đó ta có:
limf(xn)=lim(x2n−1)=limx2n−1=1−1=0
⇒ limf(x) = 0.
limg(xn)=lim(xn+1)=limxn+1=2
⇒ limg(x) = 2.
b) Ta có: f(x) + g(x) = x2 – 1 + x + 1 = x2 + x
(xn) là dãy số bất kì thỏa mãn limxn = 1. Khi đó ta có:
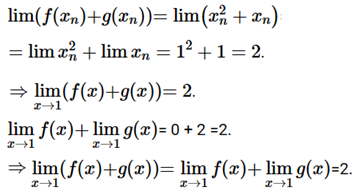
c) Ta có: f(x) – g(x) = x2 – 1 – x – 1 = x2 – x – 2
(xn) là dãy số bất kì thỏa mãn limxn = 1. Khi đó ta có:
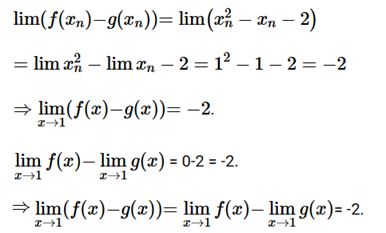
d) Ta có: f(x).g(x) = (x2 – 1)(x + 1) = x3 + x2 – x – 1
(xn) là dãy số bất kì thỏa mãn limxn = 1. Khi đó ta có:
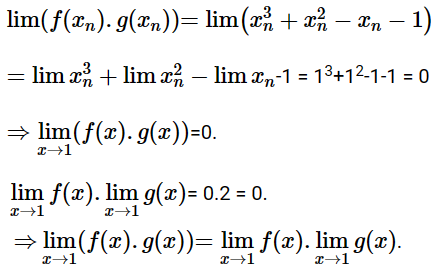
e) Ta có: 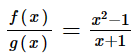
(xn) là dãy số bất kì thỏa mãn limxn = 1. Khi đó ta có:
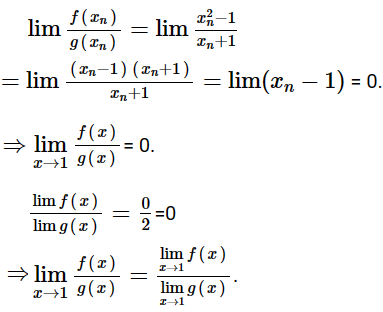
Xuất bản : 27/02/2024 - Cập nhật :
27/02/2024
Câu hỏi thường gặp
Tìm Kiếm Bài Viết
