Bài 5 trang 78 sgk Hình học 11 nâng cao

Ôn tập chương II

Bài 5 (trang 78 sgk Hình học 11 nâng cao): 

Cho hình lăng trụ tam giác A’B’C’.ABC . Gọi G, G’ lần lượt là trọng tâm của tam giác BC và A’B’C’. Một mp(α) cắt cạnh AA’, BB’, CC’, GG’ lần lượt tại A₁ ,B₁,C₁ Và G₁. Chứng minh rằng :

a) GG’ song song và bằng cạnh bên cuar hình lăng trụ;

b) G₁là trọng tâm của tam giác A₁B₁C₁;

c) G₁G' = 1/3(A₁A' + B₁B' + C₁C'); G = 1/3(A₁A + B₁B'C₁C)

Lời giải:

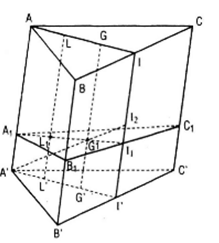
a) Gọi I , I’ lần lượt là trung điểm của các cạnh BC, B’C’ thì rõ ràng II’ song song và bằng AA’ nên tứ giác AII’A’ là hình bình hành, do đó AI song song và bằng A’I’.

c) Xét hình bình hành AII’A’. Gọi L, L’ lần lượt là trung điểm của đường thẳng AG và A’G’, L₁là giao điểm của LL’ và A₁I₁. Khi đó L₁là trung điểm của A₁G₁.

Theo định lí về đường trung bình của hình thang, ta có :

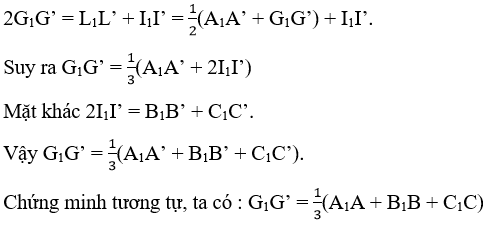
Tham khảo toàn bộ: Giải Toán 11 nâng cao