Bài 4 trang 125 sgk Hình học 11 nâng cao

Bài tập ôn cuối năm

Bài 4 (trang 125 sgk Hình học 11 nâng cao): 

Cho tứ diện ABCD . Gọi M, N lần lượt là trung điểm của BC và BD; P là một điểm thay đổi trên đoạn thẳng AD.

a) Xác định giao điểm Q của mp(MNP) và cạnh AC. Tứ giác MNPQ là hình gì ?

b) Tìm quỹ tích giao điểm I của QM và PN.

c) Tìm quỹ tích giao điểm J của QN và PM.

Lời giải:

a) Kẻ đường thẳng qua P song song với đường thẳng CD cắt AC tại điểm Q thì Q là giao điểm của AC và mp(MNP). Dễ thấy tứ giác MNPQ là hình thang (PQ // MN).

Chú ý : Nếu P ≡ A thì Q ≡ A; Nếu P ≡ D thì Q ≡ C.

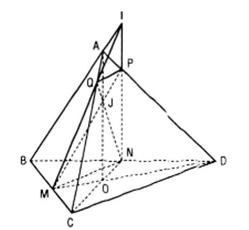
b) Thuận : Giả sử điểm I là giao điểm của QM và PN. Theo định lí về giao tuyến của ba mặt phẳng (ABC), (ABD), (MNPQ) thì điểm I thuộc đường thẳng AB.

Vì P thay đổi trên đoạn thẳng AD nên dễ thấy I chỉ nằm trên phần của đường thẳng AB trừ đi các điểm trong đoạn thẳng AB.

Đảo : Lấy 1 điểm I bất kì thuộc đường thẳng AB nhưng không nằm giữa A và B. Gọi P, Q lần lượt là giao điểm của IN với AD, của IM với AC. Khi đó rõ ràng mp(MNP) cắt AC tại Q và giao điểm của QM và PN là I.

Kết luận : Quỹ tích giao điểm I của QM và PN là đường thẳng AB trừ đi các điểm trong đoạn thẳng AB

c) Tương tự câu b), ta có quỹ tích giao điểm J của QN và QN và PM là đoạn thẳng AO(O là giao điểm của DM và CN).

Tham khảo toàn bộ: Giải Toán 11 nâng cao