Câu hỏi 1 trang 123 Toán 11 Đại số Bài 2

Bài 2: Giới hạn của hàm số

Câu hỏi 1 trang 123 Toán 11 Đại số Bài 2

Xét hàm số

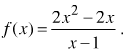
1. Cho biến x những giá trị khác 1 lập thành dãy số (x_n), x_n → 1 như trong bảng sau:

Khi đó, các giá trị tương ứng của hàm số

f(x₁), f(x₂),…, f(x_n), …

cũng lập thành một dãy số mà ta kí hiệu là (f(x_n)).

a) Chứng minh rằng 

b) Tìm giới hạn của dãy số (f(x_n)).

2. Chứng minh rằng với dãy số bất kì (x_n), x_n ≠ 1 và _xn→ 1, ta luôn có f(x_n) → 2.

(Với tính chất thể hiện trong câu 2, ta nói hàm số 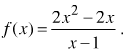 có giới hạn là 2 khi x dần tới 1).

Lời giải

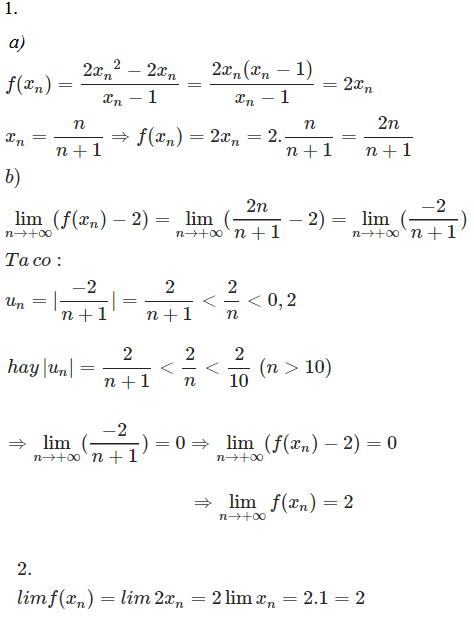
Xem toàn bộ Giải Toán 11: Bài 2. Giới hạn của hàm số