Cách ước lượng thương khi chia cho số có hai, ba chữ số

Khi dạy học sinh bài chia cho số có hai, ba chữ số trong chương trình toán lớp 4, quan trọng nhất là dạy học sinh cách ước lượng thương. Có hai cách ước lượng thương là làm tròn cả số chia và số bị chia rồi nhẩm thương hoặc lấy chữ số đầu của số bị chia chia cho chữ số đầu của số chia hoặc lấy hai chữ số đầu của số bị chia chia cho chữ số đầu của số chia (trong trường hợp chữ số đầu của số bị chia không chia hết cho chữ số đầu của số chia) để thử thương.

1. Thủ thuật ước lượng khi chia cho số có hai, ba chữ số

 Bên cạnh đó, các em cũng phải biết cách làm tròn số thông qua một số thủ thuật thường dùng. Cách làm như sau:

a) Làm tròn giảm :

Nếu số chia tận cùng là 1;2;3;4 hoặc 5 thì ta làm tròn giảm(tức là bớt đi 1;2;… hoặc 5 đơn  vị ở số chia) . Trong thực hành, ta chỉ việc che bớt chữ số tận cùng đó đi(và cũng phải che bớt chữ số tận cùng của số bị chia)

    Ví dụ 1 :

    Muốn ước lượng 92 : 23 = ?  Ta làm tròn 92 90 ; 23 20 , rồi nhẩm 90 chia 20 được 4 , ta chỉ việc láy 9 : 2 = 4, sau đó thử lại : 23 x 4 = 92 để có kết quả 92 : 23 = 4

b) Làm tròn tăng:

     Nếu số chia tận cùng là 7;8 hoặc 9 thì ta làm tròn tăng( tức là thêm 3;2 hoặc 1 đơn vị vào số chia hặc là số bị chia) trong thực hành , ta chỉ việc thêm 3 ;2 hoặc1 vào chữ số liền sau. Từ đó ta có số tròn chục để ước lượng

    Ví dụ  : Muốn ước lượng 86 : 17 = ?  Ta làm tròn 17 thành 20 và làm tròn 86 thành 90 (Vì trước đó HS đã nắm được cách chia ở các số tròn chục).

    Cách đạt tính được tiến hành như trên.

     Kết quả ước lượng 9 : 2 = 4

     Thử lại:17 x 4 =68 < 85 và 85 – 68 = 17 (ta không làm tròn nữa) nên thương ước lượng hơi thiếu do đó ta phải tăng thương đó 4 lên thành 5 rồi thử lại: 17 x 5 = 85: 86 – 85 = 1; 1 < 17 Suy ra: 86 : 17  được 5

c) Làm tròn cả tăng và giảm:

Nếu số chia tận cùng là 4; 5 hoặc 6 thì ta nên làm tròn cả tăng lẫn giảm rồi thử lại các số trong khoảng hai thương ước lượng này.

Ví dụ :  245 : 46 = ?

- Làm tròn tăng 46 thành 50 và ở số bị chia (245) thành 250. Khi đó : HS chỉ cần ước lượng 25 : 5=5 (Vì số 5 ở số bị chia và số 6 ở số chia ta đã che đi). Khi nhân vào ta có 46x5=230 (Vì 245-230=15<46 được chấp nhận).

*Lưu ý: Đã có kết quả ước lượng thương, khi nhân vào ta bỏ làm tròn.

d) Ước lượng cụ thể hóa:

Thật ra phương pháp này tôi chưa tìm cái tên để đạt cho nó, cho nên tôi tạm gọi nó là « Ước lượng cụ thể hóa ».

Ưu điểm của phương pháp này có thể chuyển phép chia cho số có nhiều chữ số thành phép cho cho số có một chũa số. Nên HS yếu có thể rèn kỹ năng bằng phương pháp này.

Ví dụ như có thể cho phép giáo viên vận dụng phương pháp áp dụng cách ước lượng cụ thể hóa bằng cách đếm có bao nhiêu chữ số ở số chia, sau đó đối chiếu ở số bị chia,những số còn lại ta dùng một tấm bìa nhỏ(có dán keo hai mặt) che dấu đi.Để rõ hơn, ta minh họa sau:

Ví dụ minh họa sau:: 5786:14=

Ta thực hiện như sau:

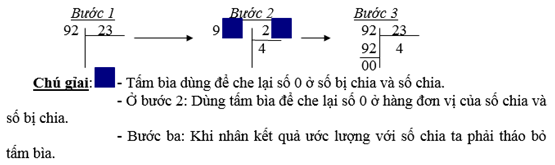
Bước 1:

*Sau khi dùng tấm bìa có kích thước phù hợp chê bớt số 786-ở số bị chia và 4 -ở số chia ta còn lại: 5:1=5. Khi nhân vào: 5x14=70. Vì 57<70, nên ta hạ kết quả ước lượng thương xuống 4.

Bước 2

 Kết quả của phép nhân úc báy giờ là: 4x14=56<57 nên kết quả này được chấp nhận – Cứ tiếp tục như vậy cho đến khi thực hiện phép tính này.

Chú ý:

 Trên thực tế việc làm việc chia cho số có hai, ba,… được tiến hành bằng thủ thuật cùng che bớt hai chữ số 2 và 3 ở hàng đơn vị để có 9 chia 2 được 4 chứ ít khi viết rõ như ở (A)

     Nếu đặt tính ta minh họa các bước như sau:

- Phương pháp ước lượng thương cụ thể hóa chỉ vận dụng đối với HS thật sự quá yếu. Nếu vận dụng một cách tràng lan dẫn đến lạm dụng,tiêu cực đối với HS có khả năng ước lượng thương đạt từ trung bình trở lên – thời điểm vận dụng tốt nhất là phụ đạo riêng HS yếu, kém.

      Trong thực tế , các việc làm trên được tiến hành trong sơ đồ của thuật tính chia (viết) với các phép thử thông qua nhân nhẩm và trừ nhẩm. Nếu học sinh chưa nhân nhẩm và trừ nhẩm thành thạo thì lúc đầu có thể cho các em làm tính vào nháp , hoặc viết bằng bút chì, nếu sai thì tẩy đi rồi điều chỉnh lại.

      Để việc làm tròn số được đơn giản , ta cũng có thể chỉ yêu cầu học sinh làm tròn số chia theo đúng quy tắc làm tròn số

2. Một số ví dụ cụ thể cách ước lượng khi chia cho số có hai, số chia có tận cùng bằng 5

Ví dụ 1: 672 : 21       

- Lượt chia thứ nhất ta lấy 67 chia cho 21; ta nhẩm thương bằng cách lấy 6 chia cho 2 được 3 lần. Thử 3 nhân 21 được 63 (hợp lí). Vậy nhận thương là 3

- Lượt chia thứ nhất dư 4 hạ 2 xuống được 42 chia cho 21; ta nhẩm thương bằng cách lấy 4 chia cho 2 được 2 lần. Thử 2 nhân 21 bằng 42 (hợp lí). Vậy nhận thương là 2

      Vậy: 672 : 21 = 32

Ví dụ 2: 855 : 45

- Lượt chia thứ nhất ta lấy 85 chia cho 45; ta nhẩm thương bằng cách lấy 8 chia cho 4 được 2 lần, thử 2 nhân 45 được 90 ( không hợp lí ) khi đó ta xuống 1 lần.

Nhưng để giảm bớt số lần thử thương thì sau khi nhẩm 8 chia 4 được 2 lần, ta nhẩm tiếp 5 chia 4 không được 2 lần. Do vậy ta xuống ngay 1 lần .

Chú ý: cách nhẩm này chỉ sử dụng trong trường hợp lấy hai chữ số của số bị chia chia cho hai chữ số của số chia

   Tương tự với các phép tính: 9009 : 33 ; 9276 : 39 .... ta cũng làm vậy

Ví dụ 3: 779 : 18

- Lượt chia thứ nhất ta lấy 77 chia cho 18. Nếu nhẩm thương bằng cách lấy 7 chia cho 1 thì thương được 7 lần nhưng khi thử lại ta phải thử thương từ 7 lần đến 4 lần mới được. Vậy để giúp học sinh giảm bớt số lần thử thương thì ta dạy học sinh nhẩm thương bằng cách làm tròn cả số chia và số bị chia. Số bị chia làm tròn thành 80, số chia làm tròn thành 20. Lấy 80 chia cho 20 được 4 lần và thử với 4 lần; 4 nhân 18 được 72 ( hợp lí) ; 77 trừ 72 được 5 hạ 9 thành 59 chia cho 18. Đến đây ta tiếp tục làm tròn 59 thành 60 còn 18 thành 20 rồi nhẩm thương 60 chia cho 20 được 3 lần, thử 3 nhân 18 bằng 54 ( hợp lí)

Vậy trong trường hợp số chia có chữ số đầu tiên là 1 và số bị chia có chữ số đầu tiên lớn hơn 5 ta nên dùng cách làm tròn cả số bị chia và số chia để nhẩm thương.

Tương tự các phép tính 6260 : 156 ; 81350 : 18

Ví dụ 4: 1154 : 62                                       

- Lượt chia thứ nhất ta lấy 115 chia cho 62; ta nhẩm thương lấy 11 chia cho 6 được 1 lần; ta thử 1 nhân 62 bằng 62, lấy 115 trừ 62 bằng 53 hợp lí. Hạ 4 xuống bằng 534 chia cho 62; ta nhẩm thương bằng cách lấy 53 chia cho 6 được 8 lần rồi thử với 8.

Ví dụ 5: 2120 : 424

- Lượt chia thứ nhất ta lấy 2120 chia cho 424; ta nhẩm thương bằng cách lấy 21 chia cho 4 được 5 lần. Thử với 5 lần là hợp lí.

Như vậy trong các phép tính chia phần lớn dạy học sinh cách ước lượng thương bằng cách lấy chữ số đầu (hoặc hai chữ số đầu) của số bị chia chia cho chữ số đầu của số chia. Chỉ một số trường hợp như trong ví dụ 3 thì ta dạy học sinh làm tròn cả số bị chia và số chia để nhẩm thương.

Ví dụ 6: Phép chia 813 : 187

- Che 2 chữ số tận cùng của số chia 187 vì 8 gần 10 làm tròn tăng 1 thành 2.

- Che 2 chữ số tận cùng của số bị chia 813 vì 1 gần 0 giữ nguyên 8 (làm tròn giảm).

- Lấy 8 : 2 được 4, nên ta ước lượng thương 813 : 187 là 4.

- Thử lại: 187 x 4 = 748, 813 – 748 = 65 , 65 < 187 (số dư < số chia)

- Vậy 813 : 187 = 4 (dư 65)

Trong thực tế khi thực hiện phép chia có phép chia làm tròn tăng cả số bị chia và số chia , nhưng cũng có phép chia vừa làm tròn tăng và giảm ở số bị chia hoặc số chia (như ví dụ trên). Còn đối với phép chia có chữ số tận cùng là 4, 5, 6 có thể làm tròn cả tăng lẫn giảm.

Ví dụ 7: Phép chia 3650 : 451

+ Làm tròn giảm :

- Che 2 chữ số tận cùng của số chia 451 còn lại số chia là 4 (làm tròn giảm).

- Che 2 chữ số tận cùng của số bị chia 3650 còn lại số bị chia là 36.

- Lấy 36 : 4 được 9, nên ta ước lượng thương 3650 : 451 là 9.

- Thử lại : 451 x 9 = 4059 > 3650, không phù hợp.

+ Làm tròn tăng:

- Che 2 chữ số tận cùng của số chia 451 còn lại 4, làm tròn tăng 4 thành 5.

- Che 2 chữ số tận cùng của số bị chia 3650 còn lại số bị chia là 36.

- Lấy 36 : 5 được 7, nên ta ước lượng thương 3650 : 451 là 7.

- Thử lại: 451 x 7 = 3157; 3650 – 3157 = 493 > 451 (số dư > số chia), chưa

phù hợp.

Có thể ước lượng thương như sau:

- Vì 7 < 8 < 9, nên ta thử với thương là 8.

451 x 8 = 3608 ; 3650 – 3608 = 42 ; 42 < 451 là phù hợp.

Vậy 3650 : 451 = 8 (dư 42).

Khi hướng dẫn học sinh thực hiện phép chia, số chia có tận cùng là 4, 5, 6 thì nên làm tròn cả tăng lẫn giảm rồi thử lại với số giữa của 2 thương vừa ước lượng (như ví dụ trên).

- Để giúp cho học sinh dễ hiểu trong việc làm tròn số (che bớt số), với số bị chia và số chia thì làm tròn giảm (số tận cùng l, 2, 3), làm tròn tăng (số tận cùng 7, 8, 9), làm tròn cả tăng lẫn giảm (số tận cùng 4, 5, 6).

Bài học về cách ước lượng thương khi chia cho số có hai, ba chữ số đã kết thúc, các con đã nhận biết được dạng bài, cách tính giá trị và vận dụng kiến thức giải các bài biểu thức có chứa một chữ. Chúc các con chăm ngoan học giỏi. Ngoài bài học này, Top lời giải còn rất nhiều nhiều bài học hay liên quan đến các dạng toán lớp 4. Hãy đăng ký để trở thành thành viên của Top lời giải để nhận nhiều tài liệu hay. Hẹn gặp lại các con ở các bài học tiếp theo!